Реализация алгоритма Metropolis-Hastings MCMC в R для случая нескольких переменных.
03 Dec 2022
Это реализация алгоритма Metropolis-Hastings MCMC, которую я применял в своих расчетах.
В виде формул я уже описывал этот алгоритм в своей статье: Султанов И.Р. Прогнозирование спредов доходности на первичном рынке российских рублевых корпоративных облигаций // Горизонты экономики. - 2019. - Vol. 1 (47). - P. 62–73. (ссылка на публикацию)
Здесь приводится непосредственно реализация алгоритма (исходный код в R).
Возможно, кому то пригодится. Удачи в ваших исследованиях.
Для написания собственной реализации алгоритма за основу взял:
- пример реализации алгоритма MCMC для случая одной переменной: Wiecki T. MCMC sampling for dummies. Available at: http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/ (accessed 20.06.2017).
- формулы для расчетов из статьи: Айвазян С.А. Байесовский подход в эконометрическом анализе // Прикладная эконометрика. - 2008. - Vol. 9. - Is. 1. - P. 93–130.
В общем виде оцениваемая эконометрическая модель может быть записана как: \[y={{\theta }_{0}}+{{\theta }_{1}}*{{x}^{(1)}}+{{\theta }_{2}}*{{x}^{(2)}}+...+{{\theta }_{k}}*{{x}^{(k)}}+\varepsilon \]
В матричной записи формула принимает вид: $$Y=X\theta +\varepsilon $$ где \(Y={{\left( {{y}_{1}},{{y}_{2}},\ldots ,{{y}_{n}} \right)}^{T}}\) – значения зависимой переменной, \(n\) – число наблюдений; \(X=\left[ \begin{matrix} 1 & x_{1}^{\left( 1 \right)} & \ldots & x_{1}^{\left( k \right)} \\ 1 & x_{2}^{\left( 1 \right)} & \ldots & x_{2}^{\left( k \right)} \\ \ldots & \ldots & \ldots & \ldots \\ 1 & x_{n}^{\left( 1 \right)} & \ldots & x_{n}^{\left( k \right)} \\ \end{matrix} \right]\) – значения независимых переменных (верхний индекс – номер переменной, нижний индекс – номер наблюдения); \(\theta ={{\left( {{\theta }_{0}},{{\theta }_{1}},\ldots ,{{\theta }_{k}} \right)}^{T}}\) – значения параметров модели, \(k\) – число переменных; \(\varepsilon ={{\left( {{\varepsilon }_{1}},{{\varepsilon }_{2}},\ldots ,{{\varepsilon }_{n}} \right)}^{T}}\) – значения остатков модели (регрессии); \(\varepsilon \in {{N}_{n}}\left( 0;\frac{1}{h}{{I}_{n}} \right)\) – распределение остатков, где \(h=\frac{1}{D\varepsilon }\), \(D\varepsilon =var\left( \varepsilon \right)\), \({{I}_{n}}\) – единичная матрица размерности \(n\).
Для определения первоначальных значений параметров, cначала рассчитывались оценки коэффициентов модели и остатки регрессии обычным методом МНК (метод наименьших квадратов) на данных за предыдущие периоды (годы).
#estimate linear regressions
m1 <- lm(f, mydata, year==2007)
m2 <- lm(f, mydata, year==2008)
m3 <- lm(f, mydata, year==2009)
m4 <- lm(f, mydata, year==2010)
m5 <- lm(f, mydata, year==2011)
m6 <- lm(f, mydata, year==2012)
m7 <- lm(f, mydata, year==2013)
m8 <- lm(f, mydata, year==2014)
#get thetas from coefficients
cf1 <- coef(m1)
cf2 <- coef(m2)
cf3 <- coef(m3)
cf4 <- coef(m4)
cf5 <- coef(m5)
cf6 <- coef(m6)
cf7 <- coef(m7)
cf8 <- coef(m8)Затем, начальные значения параметров брались, как \({{\theta }_{i}}=\frac{\sum\limits_{j=1}^{s}{\theta _{i}^{t-j}}}{s}\) – начальное значение коэффициента \(i\) (верхний индекс обозначает номер года, \(\theta _{i}^{t-j}\) - параметр \(i\) оцененный на данных за год \(t - j)\); \(h=\frac{\sum\limits_{j=1}^{s}{{{h}^{t-j}}}}{s}\) – (верхний индекс обозначает номер года); \({{\sigma }_{i}}=\sqrt{D{{\theta }_{i}}}\); \({{\sigma }_{h}}=\sqrt{Dh}\); (\(h=\frac{1}{D\varepsilon }\); \(D\varepsilon =var\left( \varepsilon \right)\)).
#primary estimations
hh <- 1/c(var(residuals(m1)),var(residuals(m2)),
var(residuals(m3)),var(residuals(m4)),
var(residuals(m5)),var(residuals(m6)),
var(residuals(m7)),var(residuals(m8)))
h <- mean(hh)
st_h <- sqrt(var(hh))Параметры модели (т.е. переменные \(\theta \) и \(h\)) рассматривались, как показатели, подчиняющиеся многомерному гамма-нормальному распределению \(E\theta =Et(2a|\theta ;\frac{\alpha }{\beta }\Lambda )\), где \(t(…,…)\) – многомерное обобщенное распределение Стьюдента. Параметры распределения рассчитывались как \(\alpha =\frac{{{h}^{2}}}{{{\sigma }_{h}}^{2}}\); \(\beta =\frac{h}{{{\sigma }_{h}}^{2}}\); \(\Lambda =\left[ \begin{matrix} {{\lambda }^{\left( 0 \right)}} & 0 & \ldots & 0 \\ 0 & {{\lambda }^{\left( 1 \right)}} & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & {{\lambda }^{\left( k \right)}} \\ \end{matrix} \right]\) (25). Где \({{\lambda }^{\left( j \right)}}=\left| \frac{1}{{{\sigma }_{j}}^{2}}\cdot \frac{\beta }{\alpha -1} \right|\)
#calc the distribution params
alpha <- (h^2)/(st_h^2)
beta <- h/(st_h^2)
ll <- length(cf1)
cfl <- matrix(0, ll, 8)
th <- matrix(0, ll, 1)
st_th <- matrix(0, ll, 1)
#L matrix calculation
L <- matrix(0, ll, ll)
for(i in 1:ll)
{
cfl[i,] <- c(cf1[i],cf2[i],cf3[i],cf4[i],cf5[i],
cf6[i],cf7[i],cf8[i])
th[i] <- mean(cfl[i,])
st_th[i] <- sqrt(var(cfl[i,]))
L[i,i] <- (1/(st_th[i]^2))*(beta/(alpha-1))
}Далее параметры модели оценивались на новых данных. Для расчетов методом Metropolis-Hastings MCMC применялась функция с названием mcmc речь о которой пойдет далее.
#get X and Y
ndata <- subset(mydata, year==2015)
M <- as.matrix(model.frame(formula=f, data=ndata))
Y <- M[,1]
X <- cbind(1,M[,-1])
n <- length(Y)
iter <- 10000
data <- mcmc(iter, X, Y, th, alpha, beta, h, L)
#get model parameters from MCMC estimation
th_sim <- matrix(0,ncol(data)-1,1)
for(i in 2:ncol(data)) th_sim[i-1] <- rbind(mean(data[,i]))Содержимое функции mcmc. Первоначальные значения параметров перед запуском алгоритма Metropolis-Hastings MCMC рассчитывались, как: \({{S}_{a}}=w*S\); \(S=\left( {{S}_{1}},\ldots ,{{S}_{i}} \right)\); \({{S}_{i}}=\frac{1}{\sqrt{{{c}_{i}}}}\); \({{c}_{i}}={{b}_{ii}}-{{B}_{i.}}B{{\left( i \right)}^{-1}}{{B}_{.i}}\); \(B=\left[ \begin{matrix} {{b}_{ii}} & {{B}_{i.}} \\ {{B}_{.i}} & B\left( i \right) \\ \end{matrix} \right]\); \(B=\frac{\alpha }{\beta }\Lambda \); \(w=1\) (позволяет регулировать процент принятия новых значений или acceptance rate).
#preliminary estimation 1
B <- h*L
C <- matrix(0, length(b_TH), 1)
for(i in 1:length(b_TH))
{
C[i] <- B[i,i]-B[i,-i]%*%solve(B[-i,-i],B[-i,i])
}
stdp <- 1/sqrt(C)Первоначальные значения элементов цепи (до запуска алгоритма) рассчитывались следующим образом: \(~M=\left( {{M}_{1}},\ldots ,{{M}_{q}} \right)\); \({{Y}_{p}}=X\theta \); \({{\vartheta }_{pr}}=var\left( Y-{{Y}_{p}} \right)\); \({{M}_{1}}=\left( {{\vartheta }_{pr}};\theta \right)\); \({{P}_{pr}}=apost\left( {{Y}_{p}};{{\vartheta }_{pr}};\theta \right)\); \({{\theta }_{pv}}=\theta \). Где \(M\) – марковская цепь; \(q\) – длина цепи; \(apost(…;…;…)\) – функция расчета апостериорной вероятности (в программе названа как aposterior).
#preliminary estimation 2
iter <- iter*1.1
b <- b_TH
pY <- X%*%b
resid <- Y-pY
sig_sq <- as.numeric(var(resid))
output=matrix(0,ncol=ncol(X)+1,nrow=iter)
output[1,]=c(sig_sq,b)
prevp <- aposterior(b, sig_sq, b_TH, alpha, beta, stdp, Y, pY)Далее, начиная со второго элемента, каждый следующий элемент последовательно рассчитывался так: \({{\theta }^{*}}=prop\left( {{\theta }_{pv}};{{S}_{a}} \right)\); \({{Y}_{p}}=X{{\theta }^{*}}\); \({{\vartheta }^{*}}=var\left( Y-{{Y}_{p}} \right)\); если \(r<\frac{apost\left( {{Y}_{p}}\;{{\vartheta }^{*}};{{\theta }^{*}} \right)}{{{P}_{pr}}}\), то {\({{M}_{i}}=\left( {{\vartheta }^{*}};{{\theta }^{*}} \right)\); \({{\vartheta }_{pr}}={{\vartheta }^{*}}\); \({{\theta }_{pv}}={{\theta }^{*}}\); \({{P}_{pr}}=apost\left( {{Y}_{p}};{{\vartheta }^{*}};{{\theta }^{*}} \right)\)} иначе {\({{M}_{i}}=\left( {{\vartheta }_{pr}};{{\theta }_{pv}} \right)\)}, где \(r\) – случайное число из равномерного распределения на отрезке \([0;1]\)}; \(prop\left( {{\theta }_{pv}};{{S}_{a}} \right)\) – функция, случайным образом генерирующая вектор чисел из нормального распределения со средними \({{\theta }_{pv}}\) и стандартными отклонениями (при этом предполагается, что отдельные числа входящие в вектор независимы между собой). При практических расчетах значения вероятностей заменялись значениями логарифмов вероятности, так как в этом случае деление вероятностей заменяется вычитанием логарифмов вероятностей и расчеты происходят значительно быстрее.
#mcmc algorithm main cycle
i <- 2
while(i<=iter)
{
bn <- propose(b, stdp)
pY <- X%*%bn
residn <- Y-pY
sig_sqn <- as.numeric(var(residn))
ace <- aposterior(bn, sig_sqn, b_TH, alpha, beta, stdp, Y, pY)
if(log(runif(1))<(ace-prevp)) {
b <- bn
sig_sq <- sig_sqn
prevp <- ace
}
output[i,]=c(sig_sq,b)
i <- i+1
}
Функция mcmc, полностью:
#mcmc simulation
#iter - number of iterations
#X, Y - curent data
#b_TH - vector of coeffients from previous data estimation
#alpha, beta - gamma distribution parameters from previous data estimation
#h, L - accuracy variables from previous data estimation
mcmc <- function(iter, X, Y, b_TH, alpha, beta, h, L)
{
#preliminary estimation 1
B <- h*L
C <- matrix(0, length(b_TH), 1)
for(i in 1:length(b_TH))
{
C[i] <- B[i,i]-B[i,-i]%*%solve(B[-i,-i],B[-i,i])
}
stdp <- 1/sqrt(C)
#preliminary estimation 2
iter <- iter*1.1
b <- b_TH
pY <- X%*%b
resid <- Y-pY
sig_sq <- as.numeric(var(resid))
output=matrix(0,ncol=ncol(X)+1,nrow=iter)
output[1,]=c(sig_sq,b)
prevp <- aposterior(b, sig_sq, b_TH, alpha, beta, stdp, Y, pY)
#mcmc algorithm main cycle
i <- 2
while(i<=iter)
{
bn <- propose(b, stdp)
pY <- X%*%bn
residn <- Y-pY
sig_sqn <- as.numeric(var(residn))
ace <- aposterior(bn, sig_sqn, b_TH, alpha, beta, stdp, Y, pY)
if(log(runif(1))<(ace-prevp)) {
b <- bn
sig_sq <- sig_sqn
prevp <- ace
}
output[i,]=c(sig_sq,b)
i <- i+1
}
return(output[-c(1:(iter/11)),])
}
Функция \(prop(...,...)\) (в программе названа как propose) функция, случайным образом генерирующая вектор чисел из нормального распределения.
#generate new varibles
propose <- function(b, st)
{
return(rnorm(length(b),mean=b,sd=st))
}
Функция \(apost(…;…;…)\), упоминавшаяся ранее, считается следующим образом: \(apost\left( {{Y}_{p}};{{\vartheta }^{*}};{{\theta }^{*}} \right)=prior\left( {{\vartheta }^{*}};{{\theta }^{*}} \right)*Like\left( {{Y}_{p}} \right)\); где \(prior\left( {{\vartheta }^{*}};{{\theta }^{*}} \right)={{P}_{g}}\left( \frac{1}{{{\vartheta }^{*}}};\alpha ;\frac{1}{\beta } \right)*\underset{i=0}{\overset{k}{\mathop \prod }}\,{{P}_{n}}\left( {{\theta }^{*}}_{i};{{\theta }_{i}};{{S}_{i}} \right)\) – априорная вероятность; \(Like\left( {{Y}_{p}} \right)=\underset{i=1}{\overset{n}{\mathop \prod }}\,{{P}_{n}}\left( {{Y}_{p}}_{i};{{Y}_{i}};\sqrt{var\left( Y \right)} \right)\) – функция правдоподобия; \({{P}_{g}}\left( \frac{1}{{{\vartheta }^{*}}};\alpha ;\frac{1}{\beta } \right)\) – функция, возвращающая значения функции гамма-распределения с параметрами \(\alpha\) и \(\frac{1}{\beta }\); \({{P}_{n}}\left( {{\theta }^{*}}_{i};{{\theta }_{i}};{{S}_{i}} \right)\) – функция, возвращающая значения функции нормального распределения с средней \({{\theta }_{i}}\) и стандартным отклонением \({{S}_{i}}\). При практических расчетах значения вероятностей заменялись значениями логарифмов вероятности, так как в этом случае перемножение вероятностей заменяется суммированием логарифмов вероятностей и расчеты происходят значительно быстрее.
#aprior likelyhood
prior <- function(b, sig_sq, b_TH, alpha, beta, stdp)
{
dn <- dnorm(b, mean=b_TH, sd=stdp, log=T)
dg <- dgamma(1/sig_sq, shape=alpha, scale=1/beta, log=T)
return(sum(dn)+dg)
}
#likelyhood function
likelyhood <- function(b, Y, pY)
{
st <- sqrt(var(pY))
dn <- dnorm(Y, mean = pY, sd = st, log = T)
return(sum(dn))
}
#aposterior likelyhood
aposterior <- function(b, sig_sq, b_TH, alpha, beta, stdp, Y, pY)
{
return(prior(b, sig_sq, b_TH, alpha, beta, stdp)+likelyhood(b, Y, pY))
}
Код программы полностью (скачать).
#Metropolis-Hastings MCMC algorithm implementation
#https://bigiskander.github.io/mcmc.html
#author: Sultanov Iskander
# BigIskander@gmail.com
#aprior likelyhood
prior <- function(b, sig_sq, b_TH, alpha, beta, stdp)
{
dn <- dnorm(b, mean=b_TH, sd=stdp, log=T)
dg <- dgamma(1/sig_sq, shape=alpha, scale=1/beta, log=T)
return(sum(dn)+dg)
}
#likelyhood function
likelyhood <- function(b, Y, pY)
{
st <- sqrt(var(pY))
dn <- dnorm(Y, mean = pY, sd = st, log = T)
return(sum(dn))
}
#aposterior likelyhood
aposterior <- function(b, sig_sq, b_TH, alpha, beta, stdp, Y, pY)
{
return(prior(b, sig_sq, b_TH, alpha, beta, stdp)+likelyhood(b, Y, pY))
}
#generate new varibles
propose <- function(b, st)
{
return(rnorm(length(b),mean=b,sd=st))
}
#mcmc simulation
#iter - number of iterations
#X, Y - curent data
#b_TH - vector of coeffients from previous data estimation
#alpha, beta - gamma distribution parameters from previous data estimation
#h, L - accuracy variables from previous data estimation
mcmc <- function(iter, X, Y, b_TH, alpha, beta, h, L)
{
#preliminary estimation 1
B <- h*L
C <- matrix(0, length(b_TH), 1)
for(i in 1:length(b_TH))
{
C[i] <- B[i,i]-B[i,-i]%*%solve(B[-i,-i],B[-i,i])
}
stdp <- 1/sqrt(C)
#preliminary estimation 2
iter <- iter*1.1
b <- b_TH
pY <- X%*%b
resid <- Y-pY
sig_sq <- as.numeric(var(resid))
output=matrix(0,ncol=ncol(X)+1,nrow=iter)
output[1,]=c(sig_sq,b)
prevp <- aposterior(b, sig_sq, b_TH, alpha, beta, stdp, Y, pY)
#mcmc algorithm main cycle
i <- 2
while(i<=iter)
{
bn <- propose(b, stdp)
pY <- X%*%bn
residn <- Y-pY
sig_sqn <- as.numeric(var(residn))
ace <- aposterior(bn, sig_sqn, b_TH, alpha, beta, stdp, Y, pY)
if(log(runif(1))<(ace-prevp)) {
b <- bn
sig_sq <- sig_sqn
prevp <- ace
}
output[i,]=c(sig_sq,b)
i <- i+1
}
return(output[-c(1:(iter/11)),])
}
#dencity plot
dence <- function(data)
{
cc <- ncol(data)
if(cc>3)
{
mm <- round(cc/3,0)
if(mm<cc/3) mm <- mm+1
par(mfrow=c(mm,3))
} else {
par(mfrow=c(1,cc))
}
#dencity
for(i in 2:cc)
{
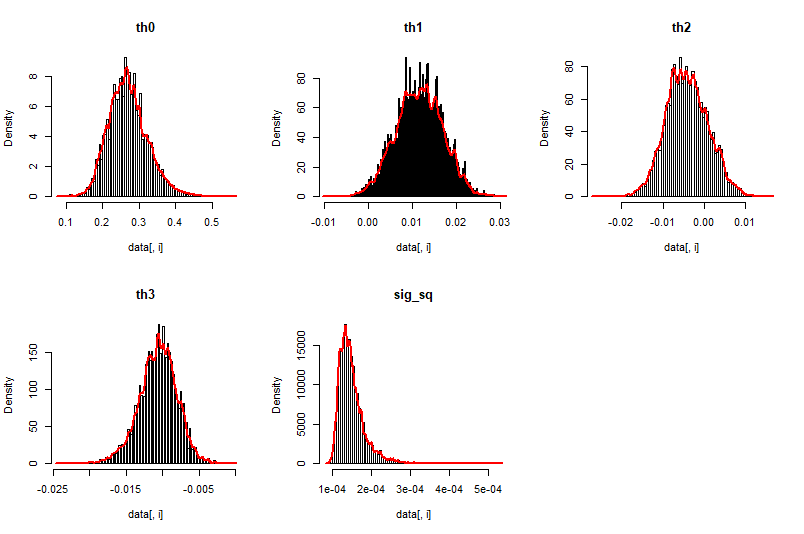
hist(data[,i],breaks=150,main=paste0("th",(i-2)),freq=FALSE)
lines(density(data[,i],bw="nrd",
kernel="gaussian"),col="red",lwd=2)
}
i <- 1
hist(data[,i],breaks=150,main="sig_sq",freq=FALSE)
lines(density(data[,1],bw="nrd",kernel="gaussian"),col="red",lwd=2)
}
#example how you can calculate variables necessary for the algorithm
#and make calculations using this implementation of MCMC algorithm
#load the data
library(foreign)
#file with data saved in stata format (not provided)
mydata <- read.dta("D:/Учеба/ВШЭ Аспирантура/Science/Calc in Stata/470.dta")
#econometric model for estimation (for example only)
f <- "YS~Leverage+LN_Maturity+LN_Issue"
# 2014 excluded because of too smal number of observations
#estimate linear regressions
m1 <- lm(f, mydata, year==2007)
m2 <- lm(f, mydata, year==2008)
m3 <- lm(f, mydata, year==2009)
m4 <- lm(f, mydata, year==2010)
m5 <- lm(f, mydata, year==2011)
m6 <- lm(f, mydata, year==2012)
m7 <- lm(f, mydata, year==2013)
#m8 <- lm(f, mydata, year==2014)
#get coefficients (theta)
cf1 <- coef(m1)
cf2 <- coef(m2)
cf3 <- coef(m3)
cf4 <- coef(m4)
cf5 <- coef(m5)
cf6 <- coef(m6)
cf7 <- coef(m7)
#cf8 <- coef(m8)
#primary estimations
hh <- 1/c(var(residuals(m1)),var(residuals(m2)),
var(residuals(m3)),var(residuals(m4)),
var(residuals(m5)),var(residuals(m6)),
var(residuals(m7)))#,var(residuals(m8)))
h <- mean(hh)
st_h <- sqrt(var(hh))
#calc the distribution params
alpha <- (h^2)/(st_h^2)
beta <- h/(st_h^2)
ll <- length(cf1)
cfl <- matrix(0, ll, 7) #8
th <- matrix(0, ll, 1)
st_th <- matrix(0, ll, 1)
#L matrix calculation
L <- matrix(0, ll, ll)
for(i in 1:ll)
{
cfl[i,] <- c(cf1[i],cf2[i],cf3[i],cf4[i],cf5[i],
cf6[i],cf7[i])#,cf8[i])
th[i] <- mean(cfl[i,])
st_th[i] <- sqrt(var(cfl[i,]))
L[i,i] <- (1/(st_th[i]^2))*(beta/(alpha-1))
}
#get X and Y
ndata <- subset(mydata, year==2015)
M <- as.matrix(model.frame(formula=f, data=ndata))
Y <- M[,1]
X <- cbind(1,M[,-1])
n <- length(Y)
#estimate using MCMC
iter <- 1000000
data <- mcmc(iter, X, Y, th, alpha, beta, h, L)
#get model parameters from MCMC estimation
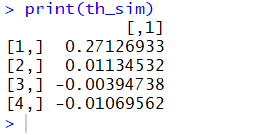
th_sim <- matrix(0,ncol(data)-1,1)
for(i in 2:ncol(data)) th_sim[i-1] <- rbind(mean(data[,i]))
print(th_sim)
#plot dencity graphs
dence(data)
Результат вычислений на моих данных приведенным выше кодом (только для примера):